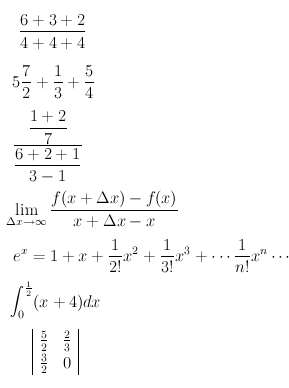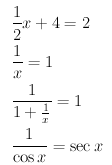
\frac{}{}を使用します。前の括弧の中には分子を、後ろの括弧の中には分母をいれます。
\frac{分子}{分母}
\frac{1}{2}x+4=2
\frac{1}{x}=1
\frac{1}{1+\frac{1}{x}}=1
\frac{1}{\cos x}=\sec x
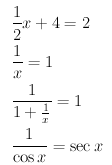
括弧の大きさを調節するには、\leftと\rightを使用します。括弧を開く前に\leftをおいて、括弧をとじる前に\rightをおきます。つまり、\left( … \right)、というかたちになります。下の二つの例を比べて下さい。
y=(\frac{1}{2}x+3)x+2
\int^1_{-2} y dx=[\frac{1}{3}x^3+4x]^1_{-2}
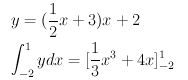
y=\left(\frac{1}{2}x+3\right)x+2
\int^1_{-2} y dx=\left[\frac{1}{3}x^3+4x\right]^1_{-2}
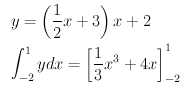
\frac{}{}を使用することによって、微分の表記も可能です。
\frac{dy}{dx}=2x^2+3x+1
\frac{d^2y}{dx^2}=4x+3
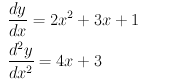
参考:微分
さて、分数を使って複雑な式を書こうとすると、表示が乱れることがあります。例えば、
\frac{1}{1+\frac{1}{x}}
\frac{\sum^{\infty}_{n=1}(n+2)^2}{n!}
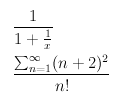
前者は分母が潰れて表示され、後者は分子のシグマが巧く表示されていません。分数を使用したときのこのような不都合を回避するためには、\displaystyleを分子、分母の前におきます。
\frac{\displaystyle 1}{\displaystyle 1+\frac{1}{x}}
\frac{\displaystyle \sum^{\infty}_{n=1}(n+2)^2}{\displaystyle n!}
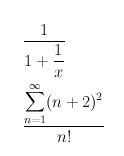
分数は数式の様々なところで使用されますので、いろいろなパターンを練習しておくといいと思います。
\frac{6+3+2}{4+4+4}
5\frac{7}{2}+\frac{1}{3}+\frac{5}{4}
\frac{\displaystyle \frac{1+2}{7}}{\displaystyle \frac{6+2+1}{3-1}}
\lim_{\Delta x \rightarrow \infty} \frac{f(x + \Delta x) - f(x)}{x + \Delta x -x}
e^x = 1 + x + \frac{1}{2!}x^2 + \frac{1}{3!}x^3 + \cdots \frac{1}{n!}x^n \cdots
\int^\frac{1}{2}_{0}(x+4) dx
\begin{array}{|cc|}
\frac{5}{2} & \frac{2}{3} \\
\frac{3}{2} & 0
\end{array}